Guía rápida para la notación Big O

El código siempre debe de ser una combinación acercada a la estabilidad entre el rendimiento y la misma resolución del problema.

Muchas veces como programadores solemos preocuparnos por la solución más rápida que nos pueda llegar a la cabeza, es lo más lógico. Nuestro objetivo principal es enriquecer las vidas de nuestros usuarios. Este concepto es el que le halla sentido al vender producto que sea ideal y escalable.

Cuando pensamos en el rendimiento, persisten muchas dudas para cuestionar el “poder” o capacidad de nuestro código.

Veámoslo de la siguiente manera:

• En el mejor escenario, ¿qué tan rápido será mi código?
• En el peor escenario, ¿qué tan lento será mi código?

Aprovecharé mi primera publicación para enfocarme en ese último caso, que es conocido como la notación Big-O

¿Qué es Big-O?

La notación Big-O nos ayuda a medir nuestro algoritmo en el peor escenario.

Nos ayuda mucho principalmente porque responde preguntas como:

• ¿Cuánto tiempo tomará mi algoritmo para ordenar algo a medida que crece el tamaño de mi conjunto de datos?

• ¿Cuánto espacio ocupará mi código para resolver un problema?

Estos escenarios pueden ser iterar sobre un array, asignar un valor a una variable o agregar entradas a una estructura de datos, por ejemplo.

Diferentes algoritmos o estructuras de datos pueden resolver cada uno de estos casos con sus respectivos compromisos.

Big-O nos brinda una forma de entender estos compromisos para abordar el problema de manera razonable.

Reglas de Big-O

Regla 1: Ignorar las constantes

Big-O se trata de cómo escalan los algoritmos. Los valores constantes no son relevantes, ya que no hacen una diferencia masiva en el resultado final.

Regla 2: Ignorar términos de bajo orden

Cuando necesitamos comparar diferentes órdenes que ocurren en un algoritmo, Big-O prefiere los términos de orden superior.

Recuerda: Big-O se trata de los casos peores.

Veamos las complejidades de Big-O más comunes:

O(1) - Tiempo Constante

Un algoritmo tiene una complejidad O(1) cuando siempre tarda el mismo tiempo en ejecutarse, sin importar el tamaño de nuestros datos. Es el mejor de los casos.

public class ConstantTimeExample {
    public static void main(String[] args) {
        int[] array = {1, 2, 3, 4, 5};
        int firstElement = array[0]; // Acceso al primer elemento.
        System.out.println(firstElement);
    }
}

O(logn) - Tiempo Logarítmico

¡Este es un poco complicado de explicar! Pero una forma fácil de entenderlo es: si nuestro algoritmo tiene una forma de dividir un problema y, por lo tanto, llegar a un resultado en menos pasos, podríamos decir que este algoritmo tiene una complejidad O(log n).

public class LogarithmicTimeExample {
    public static void main(String[] args) {
        int[] sortedArray = {1, 3, 5, 7, 9, 11, 13, 15, 17};
        int target = 11;
        int result = binarySearch(sortedArray, target);
        System.out.println("El índice del elemento " + target + " es: " + result);
    }

    static int binarySearch(int[] array, int target) {
        int left = 0;
        int right = array.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (array[mid] == target) return mid;
            if (array[mid] < target) left = mid + 1;
            else right = mid - 1;
        }
        return -1;
    }
}

O(n) - Tiempo Lineal

Un algoritmo tiene una complejidad O(n) cuando su rendimiento crece linealmente según el conjunto de datos. Depende únicamente de la cantidad de información que reciba dicha función.

public class LinearTimeExample {
    public static void main(String[] args) {
        int[] array = {1, 2, 3, 4, 5};
        for (int num : array) {
            System.out.println(num);
        }
    }
}

O(n log n) - Tiempo Linealítico

Cuando un algoritmo ejecuta una función logarítmica por operación lineal, podemos decir que su complejidad es O(n log n). La mayoría de las operaciones de ordenamiento, como quicksort o mergesort, tienen una complejidad de O(nlogn).

O(n^2) - Tiempo Cuadrático

Un algoritmo tiene una complejidad O(n^2) cuando su rendimiento depende de una operación lineal anidada. Un caso típico es cuando iteramos sobre una lista y, dentro de esta operación, iteramos sobre la misma lista nuevamente.

O(2^n) - Tiempo Exponencial

Un algoritmo tiene una complejidad O(2^n) cuando crece el doble por entrada en el conjunto de datos. Un escenario común para llegar a un tiempo exponencial es cuando aplicamos operaciones recursivas, es más, el algoritmo recursivo más famoso tiene una notación de tiempo exponencial, el famoso: Fibonacci recursivo.

O(n!) - Tiempo Factorial

Podemos encontrar esta complejidad cuando trabajamos con permutaciones y combinaciones. ¡Ten cuidado! ¡Esta complejidad crece extremadamente rápido! Se podría decir que este es el peor de los casos.

Uniendo todas las piezas

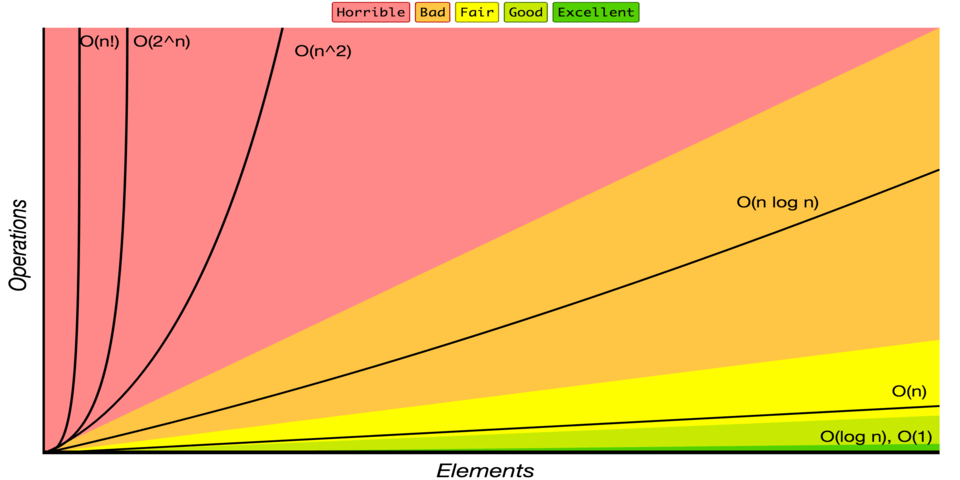
Este gráfico representa el costo de cada complejidad a través de los datos insertados en dicho algoritmo.

Ya que ahora entendemos cada una de ellas podemos realizar un análisis y orden para escoger la complejidad final del peor de los casos cuando es momento de decidir entre todas las opciones que pueden existir en una única función

O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O (2^n) < O(n!)

Tener en cuenta

Cuando creamos una misma función, esta puede representar distintas complejidades en notación Big-O.

Es decir, podemos tener una función que contenga complejidad constante que sería la asignación de una constante y al mismo tiempo esa función podría tener doble iteración de un búcle, por ende eso haría que el método por completo tuviese una complejidad cuadrática: O(n^2)

Y sí le añadimos recursividad, ahora dicho algoritmo en su peor de los casos tendría la mencionada anteriormente complejidad exponencial: O(2^n)

Cosa que no estaría bien vista en un código, jaja. Lo podríamos mejorar.

¡Eso es todo! Con este artículo tienes una de las mejores herramientas para medir tus algoritmos.

Déjame saber qué tal te fue.